Transformasi Geometri
Dalam pelajaran matematika, transformasi geometri posisi awal bidang dinotasikan dengan (x, y) dan posisi akhir dinotasikan dengan (x’,y’). Selanjutnya kita akan bahas beberapa jenis transformasi geometri.
Ada empat jenis transformasi geometri yang akan dibahas yaitu:
- Translasi (pergeseran)
- Refleksi (pencerminan)
- Rotasi (perputaran)
- Dilatasi (perkalian)
1. Translasi


2. Refleksi

Rumus untuk menentukan transformasi refleksi terhadap sumbu X adalah sebagai berikut:

Rumus transformasi refleksi terhadap sumbu Y dapat ditulis sebagai berikut:

Rumus transformasi refleksi terhadap garis y = x dapat ditulis sebagai berikut:

Rumus transformasi refleksi terhadap garis y = -x adalah sebagai berikut:
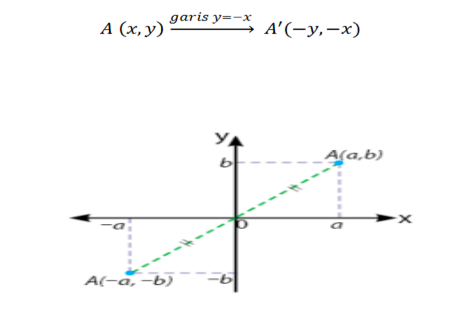
Rumus transformasi refleksi terhadap garis O(0,0) dapat ditulis sebagai berikut:

Transformasi refleksi terhadap garis y = k (k dapat bernilai sembarang) adalah sebagai berikut:

3. Rotasi
Rotasi (perputaran) adalah transformasi dengan proses memutar sembarang titik lain terhadap titik tertentu. Suatu rotasi ditentukan oleh tiga buah unsur yaitu:
- Titik pusat rotasi (apakah acuannya adalah sumbu koordinat O(0,0) atau acuannya titik sembarang P(m,n).
- Besar sudut rotasi menentukan jauhnya rotasi. Ukuran sudut rotasi dapat ditentukan dalam derajat (0), radian (rad), atau bilangan pecahan terhadap satu putaran penuh.
- Arah sudut rotasi. Suatu rotasi dikatakan mempunyai arah positif (+), jika rotasi itu berlawanan dengan arah jarum jam, sedangkan rotasi dikatakan mempunyai arah negatif (-), jika rotasi itu searah dengan arah putaran jarum jam.

Rumus untuk menentukan rotasi dari gambar di atas dapat dinyatakan dalam sebuah matriks sebagai berikut:
Dimana x’ adalah hasil rotasi terhadap titik x, y’ adalah hasil rotasi terhadap titik y, sedangkan x adalah titik awal horizontal dan titik y adalah titik awal vertikal.
Rumus untuk menentukan rotasi terhadap pusat yang sembarang (m,n) adalah sebagai berikut:
4. Dilatasi
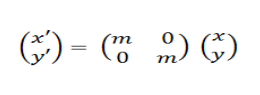
Dilatasi dikatakan diperbesar apabila m > 1 sedangkan dilatasi dikatakan diperkecil apabila m < 1.
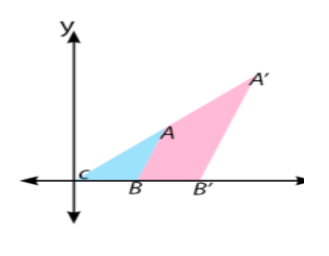
Rumus transformasi dilatasi dengan pusat rotasi O(0,0) adalah sebagai berikut:
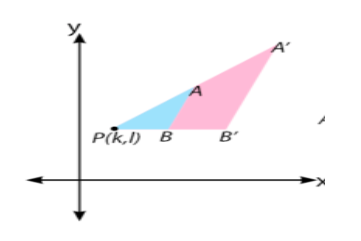
Persamaan transformasi dilatasi dengan pusat rotasi P(k,l) adalah sebagai berikut:
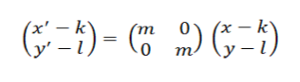
UNtuk Kelengkapan Materi dan soal dapat di Klik


Posting Komentar untuk "Transformasi Geometri"